Modern analysis instruments provide a deluge of measurement data. Automatic data processing is necessary to obtain relevant information. But: what is smart software that filters the data stream on important information and how can this properly be visualised? A short course in data reduction for the laboratory.
Many analysis techniques in the chemical laboratory have a spectroscopic or chromatographic nature. The resulting data of such a measurement instrument is a measured signal as a function of wavelength or retention time. This raw data often takes the form of a hilly landscape with sharp or blunt peaks.
Between measuring the data and assigning a certain meaning to the measurement results lies the field of data processing. An important step is to reduce the raw data to an ordered pattern. Analysis software helps here. Visualisation software presents this information so that structure, patterns and trends emerge. Interactive combined analysis-visualisation software makes it possible to navigate through the data in a convenient way.
Noise reduction
For a good data analysis, the actual measurement signal (the peaks) must be distinguished from the undesired noise that is always present. To improve the signal-to-noise ratio, you can measure a spectrum or chromatogram several times in a row, and add the measured values point by point (sample averaging): where a measuring signal always increases when added, the noise averages.
The signal-to-noise ratio can also be improved by smoothing. The measured data points are adjusted in such a way that points that are higher than the surrounding points are lowered, and points that are lower than the surrounding points become higher. This leads to a more smooth signal. The noise is strongly suppressed while a peak in the data hardly changes.
A third possibility for noise reduction is by using the Fourier transformation of the measurement data. Transform the data from the time domain to the frequency domain by displaying it as a sum of sine and cosine waves, remove all frequencies above a certain limit, and transform the result back to the time domain. The underlying idea is that signal components only occur at low frequencies, and noise components at high frequencies.
Baseline
In order to obtain accurate measurement results in a quantitative analysis, it is necessary to remove the effects of the background or baseline, especially when the spectrum consists of many peaks or when the baseline has an irregular shape.
Sometimes the intervention of the analyst is necessary to manually indicate the position of the baseline. The analyst then indicates a number of measuring points that will result in a straight line or curve, which is subtracted from the raw data.
A good automatic method for removing baseline effects is to use derivatives of spectra. The underlying principle is that we are talking about the points of a baseline when the second derivative of the data (change in the slope of a spectral curve) is approximately equal to zero, and is constant over a certain range. The second derivative is used to distinguish between peaks and baseline in the raw data (see figures). If the baseline is determined in the above way, then a function or polynomial is fitted through the points, and the fitted baseline is subtracted from the raw data.
When the entire spectrum consists of few peaks, it is easier and more efficient not to perform the baseline subtraction, but to include it in the next step where the peaks of the spectrum are fitted.
Peak analysis
The relevant information of spectra and chromatograms is found in the measurement signals or peaks. Important are the exact location of the peak and the area below the peak or the height of the peak. The peak position determines the location (wavelength, retention time) where a signal is found, and the area below the peak determines the intensity of the measurement signal. In chromatography, for example, the peak surface area is proportional to the amount of sample material passing through the detector.
A common method for determining the position of the peaks is by using the smoothed second derivative of the measurement data. This method catches several birds with one stone: differentiating between peaks and background, determining the peak positions and finding hidden peaks. This last category of peaks cannot be found as a bump in the spectrum landscape, but as a shoulder on a larger or wider peak. The existence of a local minimum in the second derivative indicates the presence of a hidden peak (see figures).
A visually simpler way to find hidden peaks is by subtracting the clearly visible peaks from the raw measurement data. When bumps are visible in the difference, this can indicate hidden peaks.
To determine the surface area under detected peaks, the raw data is fitted with a number of predefined curves, e.g. Gaussian, Lorentz or Voigt curves. The best fit is the one where the difference between the raw data and the fitted curves is minimal. By integrating the best fitting curve, you get the surface area below the peak, and thus the intensity of the signal.
The technique of non-linear curve fitting includes a large part of the above steps, such as noise reduction, baseline fitting and fitting of (overlapping) peaks. Here, the raw data is fit in its entirety or in parts by a number of peak functions. Much data analysis software is based on non-linear curve fitting.
Interpretation of the data
In the previous steps, raw measurement data have been reduced to relevant information about the measured sample, e.g. intensity as a function of x-value. But we are not there yet. What matters now is to find out what this information actually represents.
To identify an unknown sample, the measurement data needs to be compared with a library containing stored measurement values of known compounds. Relevant data here are the positions of the peaks. Libraries can be consulted stand-alone or via the internet.
For quantitative analysis, the intensities have to be converted to concentrations or quantities. This can be done by plotting the measured intensities in a series of standards of which the concentration or quantity is known. When analysing multiple components, the ratio of the intensities of characteristic peaks is decisive for the (mass) ratio of the components. By multiplying these by the absolute quantity of the sample, the absolute quantity of each component follows.
Pattern recognition is about recognising regularities in sets of measured values, thus finding similarities and differences between different spectra. A well-known pattern recognition method is the Principal Component Analysis or PCA. Here, the spectra or chromatograms to be compared are arranged in a matrix of wavelengths etc. with corresponding intensities. By applying mathematical techniques you calculate abstract variables (the so-called principal components) that are a combination of the actually measured variables. The first principal component (PC1) describes the largest possible (statistical) variance in the matrix. The second PC describes the largest possible remaining variance. So does PC3 etc. until all the variance in the data is described. The aim is to describe as much information as possible from the original spectra with as few PCs as possible. Using these PCs, similarities and differences in a set of spectra are made visible in a two- or three-dimensional plot, where individual spectra are shown as points. Such a plot is used to gain insight into the diversity within a set of spectra. In biotechnology, PCA provides a simple way to find outliers in DNA data, to find genes that behave differently and therefore ‘more interestingly’ than most genes in a set of experiments. The plots are also used for classification: groups of spectra with a lot of similarity are recognisable as clusters. In this way, analytical variables can be found that are significant for monitoring water quality, so that the number of analyses and hence the analysis costs can be reduced.
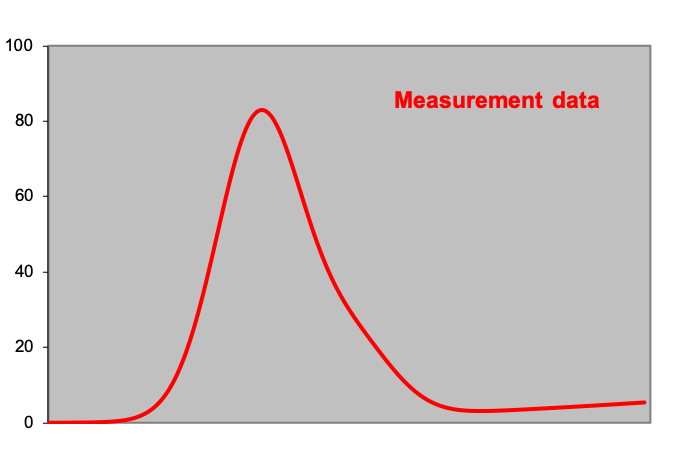
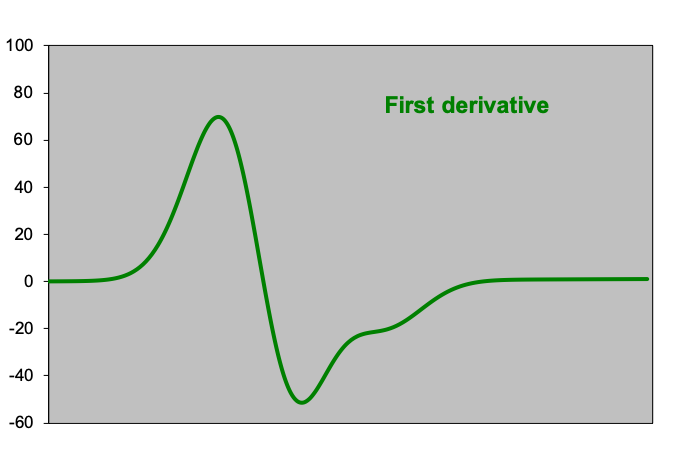
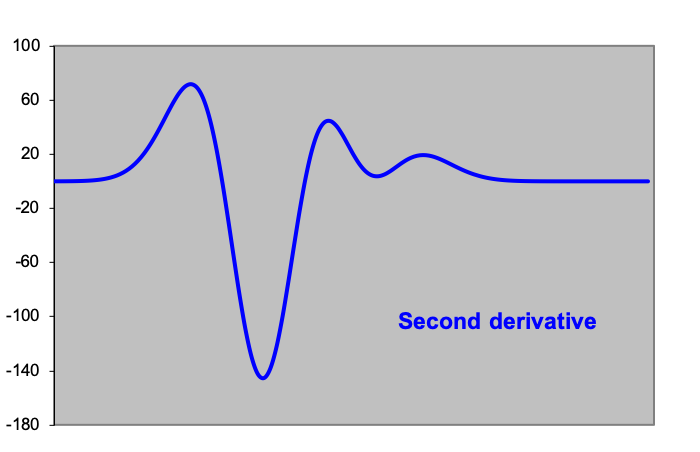
Figures: Peak analysis by means of derivatives of the measurement data: the first graph ‘measurement data’ at first sight shows one peak above a slightly ascending baseline. However, the second derivative shows two minima, indicating that there is a smaller peak to the right of the ‘large’ peak. On the left and right side of this spectrum, the second derivative is almost zero and constant; here lies the baseline.
‘Data reduction: between measuring and knowing’ was published as a (Dutch) article in the professional magazine Chemisch2Weekblad, edition 19, 11 October 2003, page 26-27.